FUNCIÓN CUADRÁTICA
1. Definición y gráfica
Una función cuadrática es aquella que puede escribirse de la forma:
| f(x) = ax2 + bx + c |
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.
La construcción del gráfico de la función cuadrática en el plano cartesiano se realiza en la misma forma que la función de primer grado: se elabora una tabla de valores, determinando así algunos puntos del gráfico, que permitan hacer un trazado de la curva.
Ejemplo 1:
Graficar la función y = x2 -2x- 3
Como se puede observar el gráfico de una función cuadrática es una curva abierta llamada parábola. Se caracteriza, a simple vista, por presentar dos ramas simétricas que se abren. La concavidad de la curva puede estar hacia arriba o hacia abajo tal como se muestra en la figura:
El ejemplo anterior la parábola de color rojo presenta la concavidad hacia abajo, es decir, que sus ramas hacia abajo.
Estas formas pueden encontrarse en la naturaleza.
2. Característica de la función cuadrática.
Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)
Otra característica o elemento fundamental para graficar una función cuadrática la da el valor o los valores que adquiera x, los cuales deben calcularse.
Ahora, para calcular las raíces (soluciones) de cualquier función cuadrática calculamos
f (x) = 0
Esto significa que las raíces (soluciones) de una función cuadrática son aquellos valores de x para los cuales la expresión vale 0; es decir, los valores de x tales que y = 0; que es lo mismo que f(x) = 0.
En tal sentido, la expresión que contiene a la variable independiente "x" hacemos:
ax² + bx +c = 0
Como la ecuación ax² + bx +c = 0 posee un
término de segundo grado, otro de primer grado y un término constante,
no podemos aplicar las propiedades de las ecuaciones, entonces, para
resolverla usamos la fórmula:
Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas).
Respecto a esta intersección, se pueden dar tres casos:
- Que corte al eje X en dos puntos distintos.(Discrimante mayor a cero, sus solucines son reales)
- Que corte al eje X en un solo punto. (Discriminante igual a cero, sus soluciones son reales e iguales)
- Que no corte al eje X. (Discriminante menor a cero, sus soluciones son cantidades complejas).
Esta característica se puede determinar analizando el discriminante.
En el eje de ordenadas (Y) la primera coordenada es cero, por lo que el punto de corte en el eje de las ordenadas lo marca el valor de c (0, c).
Veamos:
Representar la función f(x) = x² − 4x + 3
El eje de las ordenadas (Y) está cortado en +3
El eje de las ordenadas (Y) está cortado en −3
Observando la parábola siempre cortará al eje de las ordenadas (Y)a diferencia de eje de abscisas (X).
Eje de simetría o simetría
Otra característica o elemento de la parábola es su eje de simetría.
El eje de simetría de una parábola es una recta vertical que divide simétricamente a la curva; es decir, intuitivamente la separa en dos partes congruentes. Se puede imaginar como un espejo que refleja la mitad de la parábola.
Su ecuación está dada por:
De ahí se establece la ecuación del eje de simetría de la parábola:
Vértice
Como se ve en el gráfico anterior, el vértice de la parábola es el punto de corte (o punto de intersección) del eje de simetría con la parábola y tiene como coordenadas
Actividades complementarias.
1. Determina en cada una de las siguientes funciones
- La concavidad.
- Los de corte con el eje x (si los hay).
- Los punto de intersección con el eje y,
- La gráfica cada una de ellas.

2. Identifica en el contexto donde vives los objetos o fenómenos que contienen en su forma a la parábola o función cuadrática.
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org

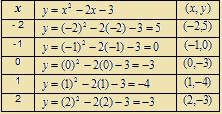








No hay comentarios:
Publicar un comentario