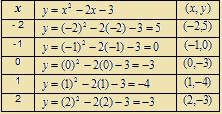sábado, 27 de julio de 2013
lunes, 15 de julio de 2013
FUNCIONES LOGARÍTMICAS
FUNCIONES LOGARÍTMICAS
A MANERA DE INTRODUCCIÓN.
PRESIÓN ATMOSFÉRICA. La presión atmosférica disminuye a medida que nos alejamos de la superficie terrestre. Al nivel del mar es de 1 atmósfera, pero, aproximadamente, por cada kilómetro que se asciende su valor es 0,9 veces la existente un kilómetro más abajo.
Forma una tabla de valores que exprese esta situación.
Altura
sobre el nivel del mar (km)
|
Presión
atmosférica (atmósferas)
|
Al
nivel del mar
|
1
|
1
|
0,9
|
2
|
0’92
= 0,81
|
3
|
0’93
= 0,729
|
4
|
0’94
= 0,656
|
5
|
0’95
= 0,590
|
6
|
0’96
= 0,531
|
...
|
...
|
x
|
0’9x
|
Veamos
ahora el problema inverso: ¿A qué altura se encontrará un globo sonda que marca
en un barómetro 0’325 atmósferas?
Si
representamos por x la altura,
tendremos que resolver la ecuación:
0,325 = 0,9x.
Para obtener una solución aproximada podemos prolongar la tabla y
vemos que el globo se encontrará entre 10 y 11 km sobre el nivel del mar.
De la ecuación anterior, el valor
exacto de x se define como el
logaritmo en base 0,9 de 0,325, como sigue:
De
lo anterior se deduce que:
x=10,66
La extraña palabra de logaritmo fue introducida a finales del siglo XVI por el matemático inglés John Naiper (1550-1617).
DEFINICIÓN
Se llaman
funciones logarítmicas a las funciones de la forma:
f(x) = loga(x)
Donde: "a" (constante) es la base del
logaritmo y "x" es la variable de la función.
Además es necesario mencionar que el logaritmo de un número se define como:

Donde: La base y
y
El número
Sabemos también que las bases más frecuentes para los logaritmos son las base 10 (logaritmos decimales) y la base el número "e=2,718281.." (logaritmos neperianos). Así las funciones más conocidas y manejadas son:

Además es necesario mencionar que el logaritmo de un número se define como:
Donde: La base
El número
Sabemos también que las bases más frecuentes para los logaritmos son las base 10 (logaritmos decimales) y la base el número "e=2,718281.." (logaritmos neperianos). Así las funciones más conocidas y manejadas son:
Gráficas
A continuación representamos
las gráficas de unas cuantas funciones logarítmicas, para una mayor comprensión
de su comportamiento.
PROPIEDADES
A partir de las gráficas presentadas anteriormente se observa el cumplimiento de las siguientes propiedades:
- La función existe sólo para valores de x mayores que 0, en consecuencia no existen logaritmos de cantidades negativas y el cero. Así el DOMINIO de la función logarítmica es R+ o el intervalo (0,∞)
- La función logarítmica cuya base del logaritmo varía entre 0<a<1, es decreciente a medida de que la variable "x" toma mayores valores.
- La función logarítmica cuya base del logaritmo varía entre 1<a<,∞ es creciente a medida de que la variable "x" toma mayores valores.
- En todos los casos la función logarítmica pasa por un punto fijo: el (1,0), es decir que la función logarítmica siempre CORTA AL EJE DE ABSCISAS en el punto (1,0).
- Observa que la función se acerca al eje Y tanto como se desee, sin llegar a cortarlo, hacia abajo en el caso en que a>1 y hacia arriba en caso de a<1 ("SIEMPRE POR LA DERECHA"), se dice por ello que: EL EJE Y ES UNA ASÍNTOTA VERTICAL-
A manera de Conclusión.
El
estudio de las funciones logarítmicas en el Nivel Secundario es de suma
importancia, para desarrollar en el estudiante conocimentos y
habilidades matemáticas que le permitan mayor comprensión de la realidad
que le rodea. Algunos ejemplos de la incidencia de las funciones logarítmicas en la naturaleza, se presentan a continuación:
Es una espiral logarítmica, se caracteriza por ser espiral equiangular o espiral de crecimiento es
una clase de curva espiral que aparece frecuentemente en la naturaleza.
Su nombre proviene de la expresión de una de sus ecuaciones.
Los
brazos de las galaxias espirales son espirales logarítmicas. La Vía
Láctea, tiene cuatro brazos espirales
mayores, cada uno de los cuales es una espiral logarítmica de 12
grados. Entre las galaxias del Universo que presentan esta
característica se puede mencionar a Andrómeda, la más cercana a nuestra
Via Láctea.
Las espirales logarítmicas se pueden encontrar en varios objetos y fenómenos de nuesro contexto como ser:
Informaciones similares podemos encontrar encontrar en:
http://covacha-matematica.blogspot.com/2011/09/todas-las-espirales-fibonacci-son.html
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org
FUNCIONES EXPONENCIALES
LA FUNCIÓN EXPONENCIAL.
Introducción.
Siempre que haya un proceso que evolucione de modo que el aumento (o disminución) en un pequeño intervalo de tiempo, sea acelerada y proporcional a lo que había al comienzo del mismo, ese proceso se describe mediante una exponencial. Por ejemplo:

Algunos tipos de bacterias se reproducen por "mitosis", dividiéndose la célula en dos cada espacios de tiempo muy pequeños, en algunos casos cada 15 minutos. ¿Cuántas bacterias se producen en estos casos, a partir de una, en un día?
Siendo x los intervalos de 15 minutos; luego x=4 en una hora, x=8 en dos horas y x=96 en un día. Así el número de bacterias en una hora es: 24=16, en dos horas 28=256 y en un día 296=79228162514264337593543950336.
Esto nos da idea del llamado ¡crecimiento exponencial!, expresión que se utiliza cuando algo crece muy deprisa.
Definición
- Crecimiento de bacterias y otras poblaciones animales o vegetales.
- Interés del dinero acumulado.
- Desintegración radiactiva

Algunos tipos de bacterias se reproducen por "mitosis", dividiéndose la célula en dos cada espacios de tiempo muy pequeños, en algunos casos cada 15 minutos. ¿Cuántas bacterias se producen en estos casos, a partir de una, en un día?
Siendo x los intervalos de 15 minutos; luego x=4 en una hora, x=8 en dos horas y x=96 en un día. Así el número de bacterias en una hora es: 24=16, en dos horas 28=256 y en un día 296=79228162514264337593543950336.
Esto nos da idea del llamado ¡crecimiento exponencial!, expresión que se utiliza cuando algo crece muy deprisa.
Definición
Se llama función exponencial de base "a" aquella cuya forma genérica es:
f (x) = ax
Siendo "a" un número positivo distinto de 1.Si la base es a=1 entonces f(x)=1; y cuando la base es negativa la función no tiene sentido en el campo de los Reales.
Por su propia definición, toda función exponencial tiene por dominio de definición el conjunto de los números reales R.
Gráficas
La gráfica de una función exponencial varía dependiendo de los valores que puedan tomar sus variables.
En primera intancia graficamos dos sencillos ejemplos de funciones exponenciales. La base es 2 en ambos casos, y el exponente que hemos tomado es x en el primer caso y –x en el segundo.
En este segundo gráfico se observa cómo el comportamiento de la función cambia tomando en cuenta los valores que asume la base "a"
- La base debe ser a > 0
- Cuando la función asume x > 0 es creciente, mientras que cuando x < 0 es decreciente, cuando es x=0 y x=1 se trata de una recta.
- Observa que la función existe para cualquier valor de "x". Decimos que la función existe siempre o que el DOMINIO de la función es todo R.
- Los valores de "y" son siempre positivos, luego la función siempre toma valores positivos para cualquier valor de "x".
- La función es creciente o decreciente, dependiendo de los valores de la base "a". Por tanto la función es creciente si a>1 y si 0<a<1 es decreciente.
- La función se acerca al eje X tanto como se desee, sin llegar a cortarlo, hacia la derecha en el caso en que a<1 y hacia la izquierda en caso de a>1 . Eso implica que el EJE X ES UNA ASÍNTOTA HORIZONTAL
La función ex.
Un caso particularmente interesante de función exponencial es:
f (x) = ex
El número e, de valor 2,7182818285..., se define matemáticamente como el límite al que tiende la expresión: (1 + 1/n)n cuando el valor de n crece hasta aproximarse al infinito. Este número es la base elegida para los logaritmos naturales o neperianos.
La función ex presenta algunas particularidades importantes que refuerzan su interés en las descripciones físicas y matemáticas de las situaciones del contexto real. Una de ellas es que coincide con su propia derivada
Actividades Complemetarias

1. Pedimos dinero en un banco y nos comprometemos a devolverlo todo a los 5 años. Nos dicen que debemos devolver exactamente el doble que lo que los dieron, ¿qué interés nos están pidiendo?
2. Se coloca un 6.000 euros al 12% de interés.
a) ¿Cuánto dinero se tendrá al cabo de 10 años?
b) ¿En cuánto tiempo se duplicará?
2. Se calcula que un bosque tiene 24000 m3 de madera y que aumenta un 3,5 % al año. ¿Cuánto tiempo tardará en duplicarse la cantidad de madera si sigue creciendo en estas condiciones? Otro bosque tiene 50000 m3 y la misma tasa de crecimiento. ¿Tardará el mismo tiempo en duplicarse? ¿Depende el tiempo de duplicación de la cantidad de madera inicial?
3. Parece ser que los piojos del cabello se reproducen duplicando su número cada 4 días. Si un niño tiene un piojo en su cabeza, y considerando que todos viven:
a) ¿Cuántos piojos tendrá dentro de 12 días ¿Y de 20 días?
b) Escribe la función y represéntala.
c) Tiene sentido unir los puntos.
d) Si en el momento inicial el niño tenía 10 piojos, contesta nuevamente a los apartados a y b.
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org
FUNCIONES CUADRÁTICAS
FUNCIÓN CUADRÁTICA
1. Definición y gráfica
Una función cuadrática es aquella que puede escribirse de la forma:
| f(x) = ax2 + bx + c |
Si representamos "todos" los puntos (x,f(x)) de una función cuadrática, obtenemos siempre una curva llamada parábola.
La construcción del gráfico de la función cuadrática en el plano cartesiano se realiza en la misma forma que la función de primer grado: se elabora una tabla de valores, determinando así algunos puntos del gráfico, que permitan hacer un trazado de la curva.
Ejemplo 1:
Graficar la función y = x2 -2x- 3
Como se puede observar el gráfico de una función cuadrática es una curva abierta llamada parábola. Se caracteriza, a simple vista, por presentar dos ramas simétricas que se abren. La concavidad de la curva puede estar hacia arriba o hacia abajo tal como se muestra en la figura:
El ejemplo anterior la parábola de color rojo presenta la concavidad hacia abajo, es decir, que sus ramas hacia abajo.
Estas formas pueden encontrarse en la naturaleza.
2. Característica de la función cuadrática.
Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)
Otra característica o elemento fundamental para graficar una función cuadrática la da el valor o los valores que adquiera x, los cuales deben calcularse.
Ahora, para calcular las raíces (soluciones) de cualquier función cuadrática calculamos
f (x) = 0
Esto significa que las raíces (soluciones) de una función cuadrática son aquellos valores de x para los cuales la expresión vale 0; es decir, los valores de x tales que y = 0; que es lo mismo que f(x) = 0.
En tal sentido, la expresión que contiene a la variable independiente "x" hacemos:
ax² + bx +c = 0
Como la ecuación ax² + bx +c = 0 posee un
término de segundo grado, otro de primer grado y un término constante,
no podemos aplicar las propiedades de las ecuaciones, entonces, para
resolverla usamos la fórmula:
Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas).
Respecto a esta intersección, se pueden dar tres casos:
- Que corte al eje X en dos puntos distintos.(Discrimante mayor a cero, sus solucines son reales)
- Que corte al eje X en un solo punto. (Discriminante igual a cero, sus soluciones son reales e iguales)
- Que no corte al eje X. (Discriminante menor a cero, sus soluciones son cantidades complejas).
Esta característica se puede determinar analizando el discriminante.
En el eje de ordenadas (Y) la primera coordenada es cero, por lo que el punto de corte en el eje de las ordenadas lo marca el valor de c (0, c).
Veamos:
Representar la función f(x) = x² − 4x + 3
El eje de las ordenadas (Y) está cortado en +3
El eje de las ordenadas (Y) está cortado en −3
Observando la parábola siempre cortará al eje de las ordenadas (Y)a diferencia de eje de abscisas (X).
Eje de simetría o simetría
Otra característica o elemento de la parábola es su eje de simetría.
El eje de simetría de una parábola es una recta vertical que divide simétricamente a la curva; es decir, intuitivamente la separa en dos partes congruentes. Se puede imaginar como un espejo que refleja la mitad de la parábola.
Su ecuación está dada por:
De ahí se establece la ecuación del eje de simetría de la parábola:
Vértice
Como se ve en el gráfico anterior, el vértice de la parábola es el punto de corte (o punto de intersección) del eje de simetría con la parábola y tiene como coordenadas
Actividades complementarias.
1. Determina en cada una de las siguientes funciones
- La concavidad.
- Los de corte con el eje x (si los hay).
- Los punto de intersección con el eje y,
- La gráfica cada una de ellas.

2. Identifica en el contexto donde vives los objetos o fenómenos que contienen en su forma a la parábola o función cuadrática.
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org
BIBLIOGRAFÍA
De Guzman, M. (1988). Matemáticas. Bachillerato 2. Grupo Editorial Anaya. Madrid - España
Goñi, J. (2000). Álgebra la Generalización de la Matemática. Editorial Ingeniería E.I.R.L. Lima - Perú.
Chungara, V. (2002). Cálculo I. Apuntes y Problemas.
www.sectormatematica.org
Suscribirse a:
Comentarios (Atom)